

Applied Mathematics and Systems Research Institute,
Research Seminar in Music, Mathematics and Computer Studies,
National Autonomous University of Mexico.
1) Introduction
Camouflage is understood in a broad sense as the process by which the appearance of a person, animal or object is changed so that it becomes difficult to distinguish from the surroundings. In nature it ranges from the development of different pigmentation patterns as in the leopard to an actual change of the colors, shapes and texture to imitate as with the chameleon or octopus. Aristotle already commented on it:
The octopus [...] seeks its prey by so changing its colour as to render it like the colour of the stones adjacent to it; it does so also when alarmed. [A]
From a biological perspective and more specifically from an evolutionary point of view, camouflage poses many interesting and intriguing questions. It is also worth noticing that from the modeling perspective, to the best of our knowledge, there are not many works devoted to the subject. However, it is natural to consider this process by means of an adaptive control system in which the aim is to match textural or optical features and a complex feedback mechanism allows to reach the target features. This observations makes it possible to discuss the problem from a mathematical and computational modeling framework. This is briefly discussed in the following section. However, we are interested in this process from an artistic point of view. So we do not intend to model or even understand the underlying biological mechanisms, but rather to propose a pattern generating system and in turn, develop a camouflage-like strategy to produce musical results.
The pattern generating system we propose is an L-system. They are also a schematic description of these systems in section three. Later on we use Markov chain to emulate, to some extent, the L-system. This can be viewed as some form of abstract camouflage in which the dynamics of a given system is imitated by another system, in this case a Markov chain. We present the elements of Markov chains we need also in section three.
Finally, in section four we applied these ideas to a concrete musical example using a SuperCollider implementation of an L-system as well as a calibrated Markov chain.
We devote the final section to concluding remarks and possible extensions of further work.
2) Mathematical Models of Camouflage
Although the biological problem seems to be fascinating, we did not find many works on the mathematical modeling of camouflage (see for instance [G] or [YSXJ]). As a general framework, from the mathematical point of view, camouflage can be viewed as an adaptive control problem. In a more precise way, given a pattern, there is a pattern generator system that, by some sort of feedback, aims at matching it. So there is an implicit comparison step in which the generated pattern is contrasted with the given one and further changes to the pattern generator are implemented until a viable degree of resemblance is achieved. This is a separate process carried out by a different subsystem which we might call a pattern analyzer. The pattern generator system in biological examples is a rather complicated and highly nonlinear structure, e.g. in an octopus, there are specialized pigment cells responsible for creating different colors, the mixing of which can produce different visual textures. The interaction and control mechanisms, the feedback process, are, to the best of our knowledge, widely unknown. That is, the mechanisms by which the matching is actually achieved are not understood. However, these must involve a rather complex optical interaction, at least for color and shape camouflage. The imitation of textures seems to be even more elusive from a biological perspective. In the following figure we present a diagram that summarizes the process.

From the mathematical point of view, the pattern generator can be very diverse: system of partial differential equations, an iterative algorithm for constructing fractals, an automaton for generating strings of characters and so on.
This last example, namely, an automaton that generates strings is particularly suited for compositional musical purposes, since it allows us to create sequences of symbols which in turn can be translated into melodic, harmonic, rhythmic or textural structures.
Notice that, as it happens with the real camouflage process, it does not imply the replication or even understanding of the underlying mechanisms generating the real pattern. It is the emulation, so to speak, of the final what is being searched.
3) Simplified Approach: L-Systems and Markov Chains
Here we describe the mathematical elements that will play the role of the given pattern, the pattern generator and pattern analyzer. We use as a given pattern a string of characters generated by a Lindenmayer system (or L-system). The system generator is provided by a Markov chain and the pattern analyzer is merely a distance function defined on strings.
Briefly, we obtain a pattern with an L-system, construct a Markov chain, with which in turn we can generate patterns and compare the result with a distance function, iterating until the generated pattern is close enough to the given one.
An example will be much more useful than an abstract explanation (adapted from https://en.wikipedia.org/wiki/L-system):
We take as a set of symbols the letters: A, B and the rules (A → AB), (B → A).
Then the initial string A will produce sequentially the following set of strings:
A
AB
ABA
ABAAB,
...
If we assign a red dot to A and a black one to B, we will generate the patterns:

As pattern generating unit we use a Markov chain. It consists of a number of states (in our case the letters A and B) and we assign to every possible transition a certain probability.
Following with our example, the possible transition would be:
A->A, A->B
B->B and B->A
We assign to every possible transition a probability. We denote them in the same order as above with:
a b
c d
We omit the details of how in our example these probabilities can actually be computed, but once this is done, we can generate strings that will camouflage the L-system. The process can be continued until the point when a certain degree of approximation is obtained.
4) A Multimedia Realization
We propose now an interactive multimedia system that imitates the biological processes of camouflage using the ideas described above and generates compositional material with the algorithmic techniques described in what follows. We start by posing the question: how would camouflage be in the auditory realm? This system has feedback from the environment through two sensors, one visual and other aural, and uses the information obtained with computer vision (real time tracking and pattern recognition) and fast Fourier transform to calibrate itself. The implementation is made with SuperCollider and Processing environments.
We emulate the camouflage process in two different ways, one as color-shape matching and the other as structure/texture matching, inspired on the behavior of some octopuses. For the color-shape type we worked mostly with a synthesis technique known as ‘spectral morphing’, which consists of the transformation of the harmonic content of a sound signal into another one interpolating them. For the structure/texture type we worked with a spatialization technique by frequency bands. We develop this proposal as a tool for assisted composition not as a piece by itself, so the data mapping presented here is just an approximation of the possibilities this paper could open.
4.1 - Color / Shape
For this system feedback we worked with a microphone as a sensor. The way we obtained information from the microphone and feed the system with data is the fast Fourier transform algorithm. We recognize color patterns through an analysis of frequency bands and took 50 bands to get the amplitude of each one of them to analyze what the microphone is listening to, so the system can imitate it. When the new sound is introduced, the system can transform it from the last harmonic shape introduced to the new one. This transformation was shaped by a technique known as morphing that can produce gradual transitions between a harmonic content to another one. The analysis of the color shapes also seeded a recursion algorithm (L-System).
4.2 - Structure / Texture
For this system feedback we worked with a digital camera as a sensor. The way we obtained information from the camera and feed the system with these data is a computer vision technique. We recognize blobs from the difference of bright and dark pixels and different locations of saturation of color in the plane RGB as well and calculate the position of their geometric centroids. The coordinates of these centroids are used by the system to project sound into space through a multichannel sound system, for this implementation we worked with a quadraphonic array.
The spatialization module that reacts to the centroids data took an audio line and divided it into ten parts with second order filters and separated them, so the first band contained all information between 1 and 2000 Hz, the second one between 2001 and 4000 Hz and so on, until reaching the 20 MHz. These bands' limits can change depending on significant saturation of energy in the spectral content. Each band had its own quadraphonic mix so they can react to the patterns recognized by the computer visualization.
We propose two different strategies of data mapping, for complex (Img. 1) and simple (Img. 2) contexts. For complex contexts we mean a context with a considerable amount of color changes. Analogously, for simple contexts we took a scale of grays. For the first one we took the coordinates of the centroids (x,y) and use them to change the quadraphonic mix of every band so the public can locate them at a specific position in space. For the second one we took the points that generate the contour of a blob and put the position of the bands in these points or went over these pads through time.
(Img. 1)
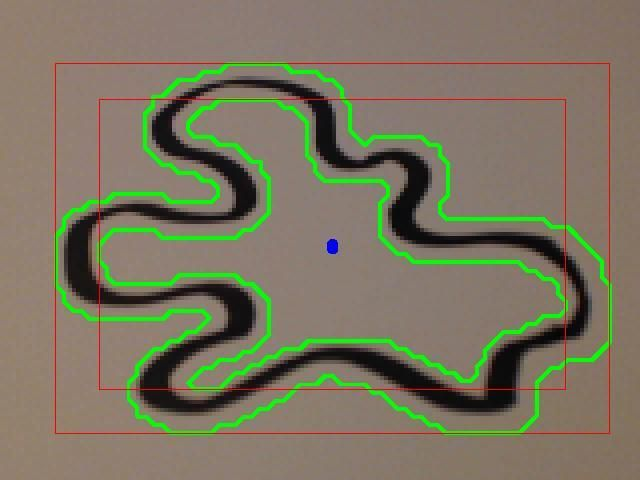
(Img. 2)

5) Conclusion
We used a mathematical approach to model the process of camouflage of a given pattern. The process itself can be used as the basis for generating sound and visual material in an integrated compositional system. Preliminary implementations were developed in SuperCollider and processing (for the sake of completeness the SuperCollider code is included at the end of the paper). In general, the platform developed here is another instance in which a mathematical model can be used to expand the creative possibilities of an artist.
References
[A] Aristotle (c. 350 BC). Historia Animalium. IX, 622a: 2–10. Cited in Borrelli, Luciana; Gherardi, Francesca; Fiorito, Graziano (2006). A catalogue of body patterning in Cephalopoda. Firenze University Press. ISBN 978-88-8453-377-7.
[G] Glendinning, Paul. The mathematics of motion camouflage. Proc Biol Sci. 2004 Mar 7; 271(1538): 477–481. doi: 10.1098/rspb.2003.2622. PMCID: PMC1691618.
[YSXJ] Yong Zhang, , Shi-qiang Xue, Xiao-jun Jiang, Jing-yang Mu, Yang Yi. The Spatial Color Mixing Model of Digital Camouflage Pattern. doi:10.1016/j.dt.2013.09.015.